Q) A boy whose eye level is 1.35 m from the ground, spots a balloon moving with the wind in a horizontal line at some height from the ground. The angle of elevation of the balloon from the eyes of the boy at an instant is 60. After 12 seconds, the angle of elevation reduces to 30°. If the speed of the wind is 3m/s then find the height of the balloon from the ground. (Use √3= 1.73)

Ans: 

Let’s start solving by making a diagram for the question:

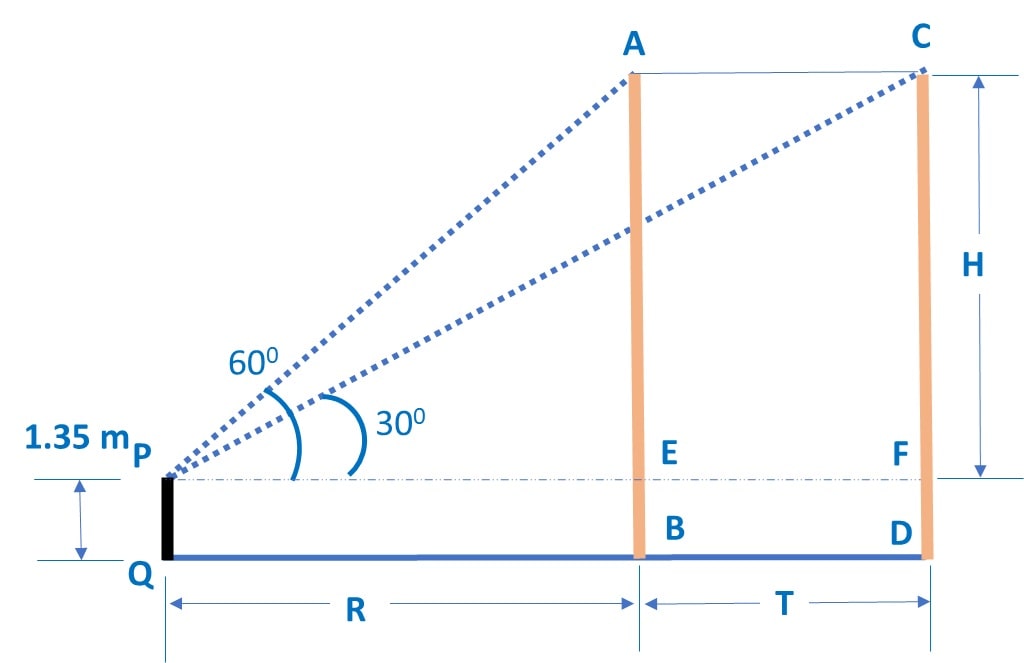
Here boy is PQ of height 1.35 m. Initially Balloon is at point A with height AB as H and distance QB as R.

After some time, balloon reaches point C and moves distance AC with the wind.

Step 1: We calculate distance travelled by balloon:

Since wind speed is 3 m /s and balloon travelled for 12 seconds,

hence distance travelled by balloon, AC = 12 x 3 =  36 m

From the diagram, AC = EF = BD = 36 m

Step 2: Let’s take in Δ AEP, tan 60 =

∴  √3 =

∴  R = …….. (i)

Step 3: Let’s take in Δ CFP, tan 30 =

∴         (∵ EF = 36 in step 1)

∴  R + 36 = H√3 ………. (ii)

Step 4: From equation (i), we put value of R into equation (ii), we get:

+ 36 = H√3

∴ H + 36 √3 = H√3 x √3

∴ 3 H – H = 36 √3

∴ H = = 18 √3

∴ H = 18 x 1.73 = 31.14 m

Since, H is the height of balloon from boy’s eye level.

∴ Height of balloon from ground = Height of balloon from eye level + Boy’s height

or we can say, CD = CF + FD

∴ CD = 31.14 + 1.35   (∵ FD = EB = PQ = 1.35 m)

∴ CD = 32.49 m

Therefore, the height of the balloon from ground level is 32.49 m

Please do press “Heart” button if you liked the solution.