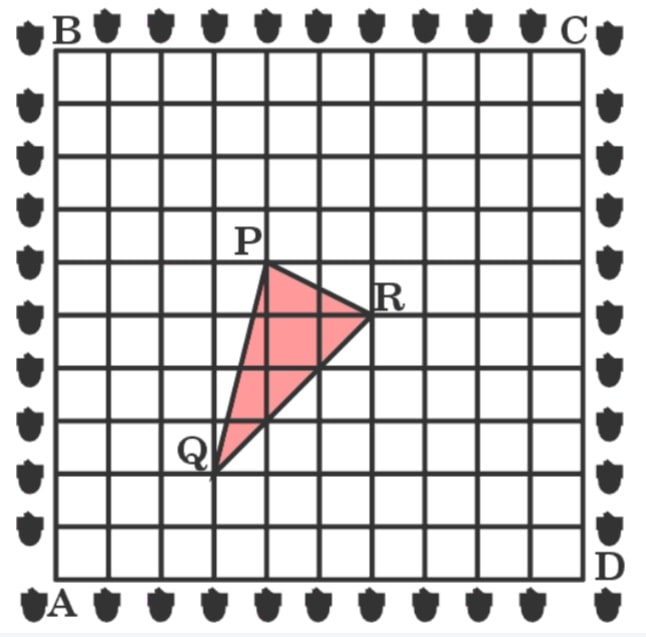
Q) A garden is in the shape of a square. The gardener grew saplings of Ashoka tree on the boundary of the garden at the distance of 1 m from each other. He wants to decorate the garden with rose plants. He chose a triangular region inside the garden to grow rose plants. In the above situation, the gardener took help from the students of class 10. They made a chart for it which looks like the given figure.
Based on the above, answer the following questions :
(i) If A is taken as origin, what are the coordinates of the vertices of Δ PQR?
(ii) Find distances PQ and QR.
(iii) Find the coordinates of the point which divides the line segment joining points P and R in the ratio 2 : 1 internally.
(iv) Find out if D PQR is an isosceles triangle.
Ans:
(i) coordinates of the vertices of Δ PQR:
from the diagram, if we take A as origin, we get following:
Coordinates of point P: (4, 6)
Coordinates of point Q: (3, 2)
Coordinates of point R: (6, 5)
(ii) Distances PQ and QR:
We know that the distance between two points P (X1, Y1) and Q (X2, Y2) is given by:
PQ = ![]()
From the diagram, we have co-ordinates as P (4, 6) and Q (3, 2)
∴ Distance PQ = ![]()
∴ PQ = ![]()
∴ PQ = √17
∴ PQ = √17 units
Similarly, from the diagram, we have co-ordinates as Q (3, 2) and R (6, 5)
∴ Distance QR = ![]()
∴ QR = ![]()
∴ QR = √18
∴ QR = 2√3 units
Therefore, the length of PQ is √17 units and QR is 2√3 units.
(iii) coordinates of the point dividing the line PR in the ratio 2 : 1 internally:
By section formula, coordinates of point P (X, Y) which lies between two points (x1, y1), (x2, y2) will be given by:
P (X,Y) = ![]()
From the given diagram, we have coordinates of points P (4, 6) and R (6, 5)
Since, the point divides the line in ratio of 2:1, therefore m1 = 2 and m2 = 1
P (X,Y) = ![]()
= ![]()
Therefore, the coordinates of the point is ![]() which divides line AB in ratio of 2:1.
which divides line AB in ratio of 2:1.
(iv) Is Δ PQR an isosceles triangle?:
If Δ PQR is an isosceles triangle, then its two sides will be equal.
Coordinates of all 3 vertices are: P(4, 6), Q(3, 2) and R(6, 5)
Therefore, let’s check length of all the 3 sides:
We know that the distance between two points P (X1, Y1) and Q (X2, Y2) is given by:
![]()
PQ = √17 units (from part (ii) above)
QR = 2√3 units (from part (ii) above)
PR = ![]()
∴ PR = ![]()
∴ PR = √5 units
Since all 3 sides are unequal, therefore Δ PQR is NOT an isosceles triangle.
Please press the “Heart”, if you liked the solution.
