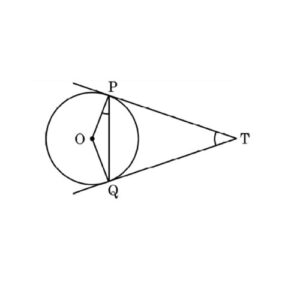
Q) Two tangents TP and TQ are drawn to a circle with centre 0 from an external point T. Prove that ∠PTQ = 2∠OPQ.
Ans:
TP = TQ
⇒ ∠TPQ = ∠TQP
Let ∠PTQ be θ
⇒ ∠TPQ = ∠TQP = ![]()
= 90° – ![]()
Now, ∠OPT = 90°
⇒ ∠OPQ = 90° – [90° – ![]() ] =
] = ![]()
![]() ∠PTQ = 2 ∠OPQ …. Hence Proved
∠PTQ = 2 ∠OPQ …. Hence Proved
