Sides AB and AC and median AM of a Δ ABC are proportional to

Q) Sides AB and AC and median AM of a Δ ABC are proportional to sides DE and DF and median DN of another Δ DEF. Show that Δ ABC ~ Δ DEF.

Ans:

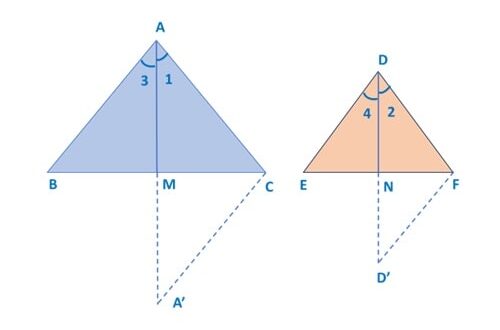
Construction: Extend AM to A’ such that AM = A’M and extend DN to D’ such that DN = D’N

Join A’C and D’F

Proof: In Δ ABM and Δ A’CM,

AM = A’M (construction)

BM = MC (M is median of BC)

∠ AMB = ∠ A’MC (vertically opposite angles)

by SAS congruence criterion, Δ ABM ≅ Δ A’CM

$\therefore$ AB = A’C [by CPCT]

Similarly, in Δ DEN and Δ D’FN, Δ DEN ≅ Δ D’FN

Therefore, DE = D’F

We know that, $\frac{AB}{DE} = \frac{AC}{DF} = \frac{AM}{DN}$

$\therefore \frac{A'C}{D'F} = \frac{AC}{DF} = \frac{\frac{AA'}{2}}{\frac{DD'}{2}}$

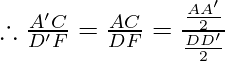
Therefore, in Δ AA’C and Δ DD’F by SSS similarity criterion, Δ AA’C ∼ Δ DD’F

∠ 1 = ∠ 2 [Corresponding angles of similar triangles are equal]

Similarly, ∠ 3 = ∠ 4

Therefore, ∠ 1 + ∠ 3 = ∠ 2 + ∠ 4

∠ A = ∠ D

In Δ ABC and Δ DEF,

We know that, $\frac{AB}{DE} = \frac{AC}{DF}$ (given)

∠ A = ∠ D (from above)

Now, by SAS similarity criterion,

Δ ABC ∼ Δ DEF ……….. Hence Proved !

Please press the “like” button if you like the solution.

Contact us