One evening, Kaushik was in a park. Children were playing cricket

Leave a Comment / Class 10th Case Study, trigonometry applications / By Sapling Academy

Q) One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°.
When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.

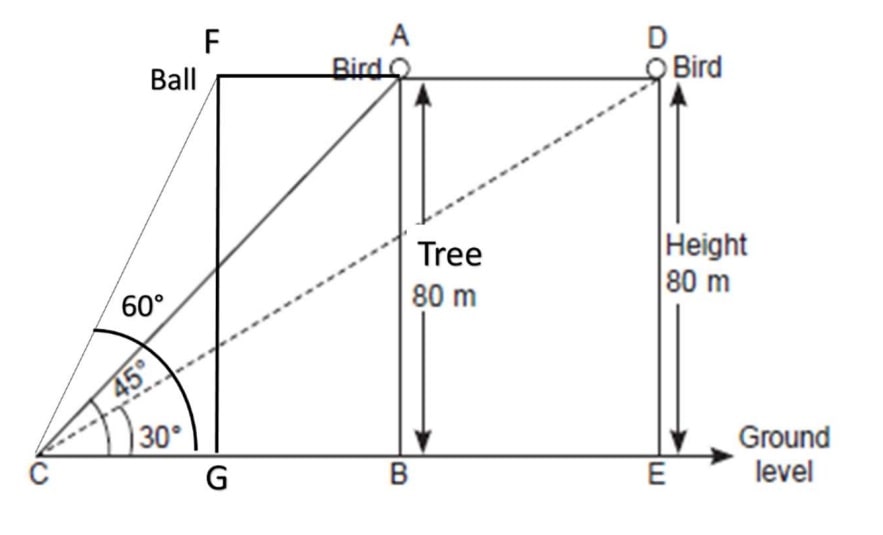
(i) At what distance from the foot of the tree was he observing the bird sitting on the tree?
(ii) How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball?
(iii) What is the speed of the bird in m/min if it had flown 20(√3 + 1) m?

Ans:

VIDEO SOLUTION

STEP BY STEP SOLUTION

(i) Distance of observer from the foot of the tree:

Since, we need to find distance BC, height of the tree is given to us.

Hence, let’s look at Δ ABC, tan 45° = $\frac{AB}{BC}$

1 = $\frac{80}{BC}$

$\therefore$ BC = 80

Therefore, the Distance of observer from the foot of the tree is 80 m.

(ii) Distance flown by the bird in the given 2 seconds time:

After the ball hits the tree, the bird flew from point A to point D in 2 seconds, and AD is the distance flown by the bird.

Hence, in Δ ADC,

tan 30° = $\frac{DE}{CE}$

Since its given that the bird’s height is same, therefore DE = AB = 80 m

Hence, $\frac{1}{\sqrt 3} = \frac{80}{CE}$

or CE = 80√3

From the given diagram, we can see that CE = CB + BE

∴ BE = CE – CB = 80√3 – 80 = 80 (√3 – 1) m

From the given diagram, its clear that AD = BE = 80 (√3 – 1) m,

Therefore, the bird flew 80 (√3 – 1) m in the given 2 seconds time.

OR

(ii) Distance travelled by ball in the sky after hitting the tree:

The ball hits the tree at point A and Kaushik saw it at point F, therefore the distance travelled by the the ball in the sky is AF.

in Δ FGC, tan 60° = $\frac{FG}{CG}$

Since its given that the ball’s height is same, therefore FG = AB = 80 m

Hence, √3 = $\frac{80}{CG}$

∴ CG = $\frac{80}{\sqrt3}$

From the given diagram, we can see that CB = CG + GB

∴ GB = CB – CG = $80 - \frac{80}{\sqrt3}$ = $80 (1 - \frac{1}{\sqrt3})$

From the given diagram, its clear that AF = GB;

Therefore, the distance travelled by ball in the sky after hitting the tree is $80 (1 - \frac{1}{\sqrt3})$ m.

(iii) Speed of the bird in m/min if it had flown 20(√3 + 1) m:

We know that the Speed = $\frac{Distance}{Time}$

Given that the bird flew the given distance of 20(√3 + 1) m in 2 sec or in $\frac{2}{60}$ mins

Therefore, bird’s speed = $\frac{20 (\sqrt 3 + 1)}{\frac{2}{60}}$ = 600 (√3 + 1) m/min

Therefore, the speed of the bird will be 600 (√3 + 1) m / min when it had flown 20(√3 + 1) m.

Please do press “Heart” button if you liked the solution.

Leave a Comment Cancel Reply