The difference between the outer and inner radii of a hollow

Leave a Comment / Class 10th, surface areas and volumes / By Sapling Academy

Q) The difference between the outer and inner radii of a hollow right circular cylinder of length 14 cm is 1 cm. If the volume of the used in making the cylinder is 176 cm³, find the outer and inner radii of the cylinder.

Ans.

Let’s draw the diagram for the given question: 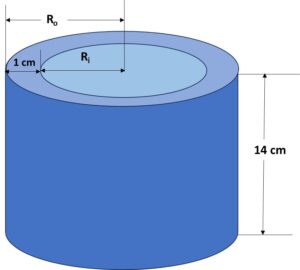The difference between the outer and inner radii of a hollow right circular cylinder of length 14 cm is 1 cm. CBSE 2024

Here, Cylinder has outer radii as $R_o$ and inner radii as $R_i$ , height 14 cm.

We know that the volume of the Cylinder, $V_c = \pi (r)^2 h$

Given that h = 14 cm

Here, outer volume $V_o = \pi (R_o)^2 (14)$

And Inner volume $V_i = \pi (R_i)^2 (14)$

From the diagram, it is clear that the difference of the outer and inner volume is the volume of the metal. It is given that metal volume is 176 cm ³

Therefore, $\pi (R_o)^2 (14) - \pi (R_i)^2 (14) = 176$

$\Rightarrow \pi (14) [(R_o)^2 - (R_i)^2] = 176$

$\Rightarrow \frac{22}{7}(14) [(R_o + R_i)(R_o - R_i)] = 176$

Given that $R_o - R_i = 1$ ……… (i)

$\Rightarrow 44[(R_o + R_i)(1)] = 176$

$\Rightarrow (R_o + R_i) = 4$ ….. (ii)

By adding Equation (i) and (ii), we get:

$(R_o - R_i) + (R_o + R_i) = 1 + 4$

$2 R_o = 5$

$R_o = \frac{5}{2}$

Substituting value of $R_o$ in equation (ii), we get:

$R_o + R_i = 4$

$\Rightarrow \frac{5}{2} + R_i = 4$

$\Rightarrow R_i = 4 - \frac{5}{2}$

$\Rightarrow R_i = \frac{3}{2}$

Therefore, the outer radii of cylinder is $\frac{5}{2}$ cm and inner radii is $\frac{3}{2}$ cm.

Please do press “Heart” button if you liked the solution.

Leave a Comment Cancel Reply