Q) In the given figure, AB is a diameter of the circle with centre O. AQ, BP and PQ are tangents to the circle. Prove that ∠POQ = 90°.

Ans: Let’s connect Point O with Point R where tangent PQ touches the circle.
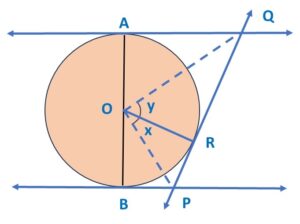
Let’s consider ∠ POR = x and ∠ QOR = y
Step 1: Let’s take Δ BOP and Δ ROP:
Here, PB = PR ( tangents from a point on a circle)
OP = OP (common side)
OB = OR (radii of same circle)
∴ Δ BOP ![]() Δ ROP
Δ ROP
∴ ∠ BOP = ∠ ROP = x ………. (i)
Step 2: Next, we take Δ QOA and Δ QOR:
Here, QA = QR ( tangents from a point on a circle)
OQ = OQ (common side)
OA = OR (radii of same circle)
∴ Δ QOA ![]() Δ QOR
Δ QOR
∴ ∠ QOA = ∠ QOR = y ……… (ii)
Step 3: Next, We can see from the diagram, that AB is a straight line.
∴ ∠ QOA + ∠ QOR + ∠ ROP + ∠ BOP = 1800
∴ y + y + x + x = 1800
∴ 2 (x + y) = 1800
∴ (x + y) = 900 …. (iii)
Step 4: ∠ POQ = ∠ ROP + ∠ ROQ = x + y
comparing with equation (iii), we get:
∠ POQ = 900
Hence Proved !
Please do press “Heart” button if you liked the solution.
