Q) A horse, a cow and a goat are tied, each by ropes of length 14 m, at the corners A, B and C respectively, of a grassy triangular field ABC with sides of lengths 35 m, 40 m and 50 m. Find the total area of grass field that can be grazed by them. 

Ans:  Let’s first draw a diagram for the given question:

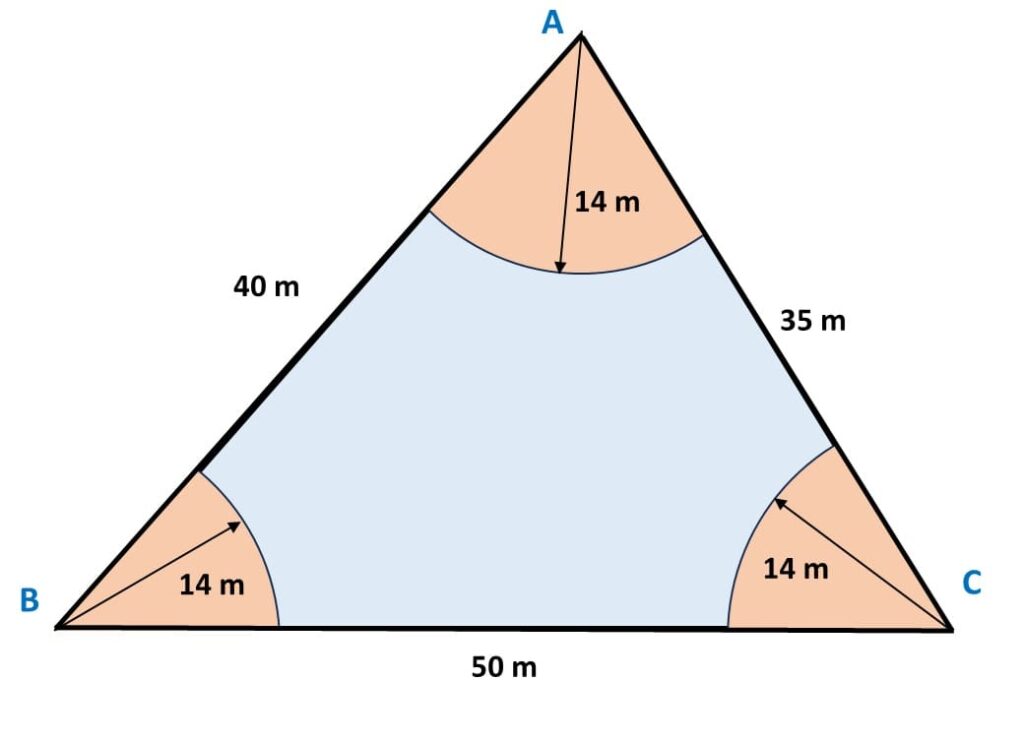
Since the animal tied up by a rope, it will graze in circular fashion where rope will become radius of that circle and the area grazed will be covered by that angle.

Hence the area grazed by that animal will be given by

Here, θ is the angle covered by the animal and R is the length of the rope (this rope makes radius of the circle)

Let’s start by calculating area grazed by each animal:

Let’s consider that Horse is tied up at point A and the angle covered by it is ∠ A

Hence, the area grazed by Horse:

Similarly, if Cow is tied up at point B and the angle covered by it is ∠ B

Hence, the area grazed by Cow:

Last, if Goat is tied up at point C and the angle covered by it is ∠ C

Hence, the area grazed by horse:

Now the total area grazed by all the three animals = Area grazed by Horse + Area grazed by Cow + Area grazed by Goat

=

=

Since A,B and C are angles of a common triangle, hence the sum of the angles A + B + C = 180⁰

Therefore, Area grazed by all 3 animals  =

=

We are given length of the rope is 14 m and this rope is the radius of the circle hence R = 14m

Therefore, total area grazed:

=

=

= 11 x 14 x 2 = 308 m²

Therefore the area grazed by all three animals is 308 m²

Please do press “Heart” button if you liked the solution.