A student was asked to make a model like a cylinder with two cones

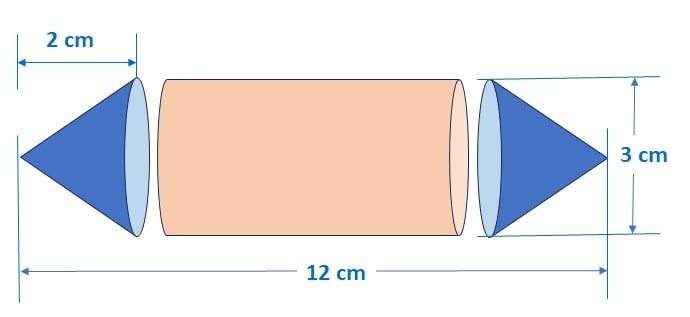
Q) A student was asked to make a model like a cylinder with two cones attached to its ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its total length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model.

Ans:

We know that, volume of the cone = $\frac{1}{3}\pi$ r² h₁. Here, r is the radius of cylinder and h₁ is the height of cylinder.

and the volume of the cylinder = $\pi$ r² h₂. Here, r is the radius of cone and h₂ is the height of cone.

[Note: Since radius is same for given cylinder and both cones, we have taken same variable of r, but since heights are different for both shapes, we have taken different variables.]

The volume of the model = volume of left cone + volume of the cylinder + volume of right cone

= $\frac{1}{3}\pi$ r²h₁ + $\pi$ r² h₂ + $\frac{1}{3}\pi$ r²h₁

= $\pi$ r² ( $\frac{1}{3}$ h₁ + h₂ + $\frac{1}{3}$ h₁)