Q) An observer 1.5 m tall is 28.5 m away from a tower and the angle of elevation of the top of the tower from the eye of the observer is
45 degrees. What is the height of the tower?
Ans:
Step 1: Let’s draw a diagram for the given question:
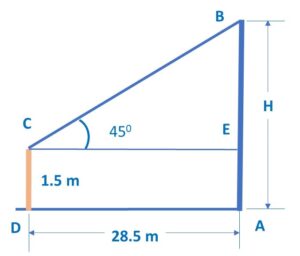
Let the tower be AB and observer be CD. The angle of elevation from point C is 45 and distance between points A and D is 28.5 m.
We need to find the value of height of tower, H.
Step 2: From the diagram, we can see that:
CD = AE = 1.5 m
Now since AB = AE + BE
∴ H = 1.5 + BE
∴ BE = H – 1.5
Step 3: In Δ BCE, tan C = ![]()
∴ tan 450 = ![]()
∴ 1 = ![]()
∴ H – 1.5 = 28.5
∴ H = 28.5 + 1.5
∴ H = 30
Therefore, the height of the tower is 30 m.
Please press “Heart” button if you like the solution.
