Evaluate: (5 cos 2 60 + 4 sec 2 30

Q) Evaluate: $\frac{5 \cos ^2 60 + 4 \sec ^2 30 - \tan ^2 45} {\sin ^2 30 + \sin ^2 60}$

Ans: Let’s take the components one by one:

Step 1: we know that cos 60 = $\frac{1}{2}$ , sec 30 = $\frac{2}{\sqrt 3}$ , tan 45 = 1,

sin 30 = $\frac{1}{2}$ , sin 60 = $\frac{\sqrt 3}{2}$

Step 2: Let’s put these values in the given expression, we get:

$\frac{5 \cos ^2 60 + 4 \sec ^2 30 - \tan ^2 45} {\sin ^2 30 + \sin ^2 60}$

∴ $\frac{5 (\frac{1}{2})^2 + 4 (\frac{2}{\sqrt 3})^2 - (1)^2} {(\frac{1}{2})^2 + (\frac{\sqrt 3}{2})^2}$

∴ $\frac{5 (\frac{1}{4}) + 4 (\frac{4}{3}) - (1)}{(\frac{1}{4}) + (\frac{3}{4})}$

∴ $\frac{(\frac{5}{4} + \frac{16}{3} - 1)}{(\frac{1}{4} + \frac{3}{4})}$

∴ $\frac{(\frac{15 + 64 - 12}{12})}{(\frac{1 + 3}{4})}$

∴ $\frac{(\frac{67}{12})}{(\frac{4}{4})}$

∴ $\frac{67}{12}$

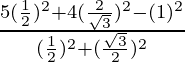
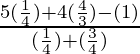
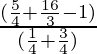
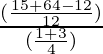
Therefore the value of given expression is $\frac{67}{12}$

Please press the “Heart”, if you like the solution.

Contact us