Q) Find the area of the unshaded region shown in the given figure.

Ans:

Let’s redraw the diagram:

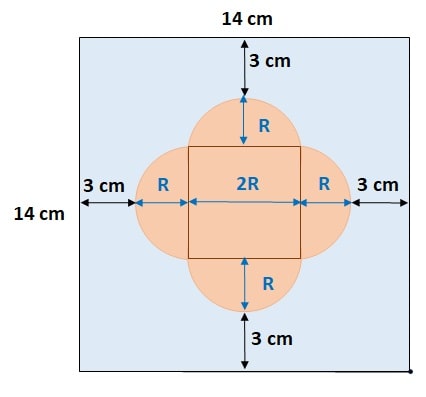
As we can see in the diagram, in the center area:

diameter of semicircle (2R) = side of the inside square (S)

or S = 2R ………………. (i)

Also we see that Side of larger square = Gap from left side + radius of left semicircle + side of inside square + radius of right semicircle + gap from right side

14 = 3 + R + S + R + 3

2R + S = 8

R = 2 cm     (S = 2R from equation (i)

and side of the square, S  = 2R = 4 cm

We can see that the area of center region = 4 x area of semicircle + area of inside square

= 4 + (S)²

= 4 + (4)²  = 8 + 16

= 8 $(\frac{22}{7}) + 16 = 41.14 cm²

Therefore, the area of unshaded region in the center is 41.14 cm².