Q) Find the mean and median of the following data:

Ans:

(i) Mean Value of data:

To calculate the mean value, let’s re-organize the data:

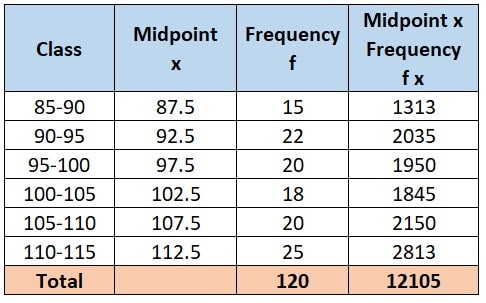
To arrange the above, we take following steps:

• We calculate midpoint ‘x’of each class by
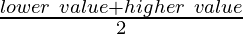
• Then we calculate ‘fx’ by multiplying midpoint of each class with frequency of that class
• We calculate Σf by summing up all the frequencies and Σfx by adding up all the values of fx

Next, we know that, mean of grouped data is given by:

Mean of grouped data =

Therefore, Mean value = = 100.875

Hence, the mean value of the given data is 100.875

(ii) Median value of data:

To calculate the median value, let’s re-organize the data:

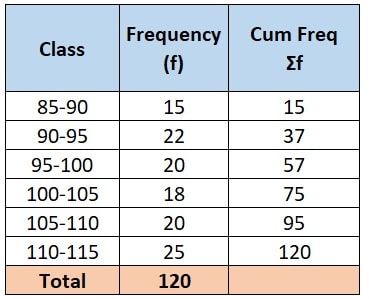
To find the median, we need to first identify middle class of the data.

• We know that, Median class is the class where the cumulative frequency crosses 50% of total of frequencies.
• Here, in the given data, total of frequencies is 120 and at row 4 cumulative frequency is crossing 50% of total (i.e. 60)
• Hence, our Median class = 100-105

Next, the median value of a grouped data is given by:

Median =

Here:

L = Lower boundary of the median class = 100

n = Total number of frequencies = 120

= Cumulative frequency of the class before the median class = 57

f = Frequency of the median class = 18

h = Class width = 105 – 100 = 5

hence, the Median =

⇒ 100 + [(60 – 57)] x

⇒ 100 +

⇒ 100 + 0.833

⇒ 100.833

Therefore, Median value of the grouped data is 100.833

Please do press “Heart” button if you liked the solution.