Q) Find the ratio in which the point (8/5, y) divides the line segment joining the points (1, 2) and (2, 3). Also, find the value of y.

ns: Let’s make a diagram for the given question:

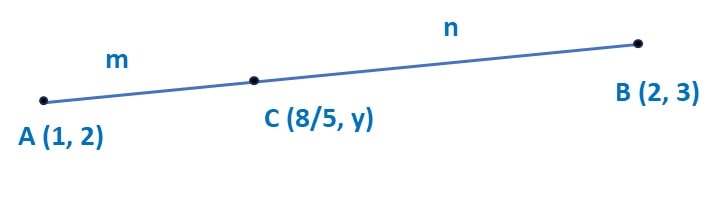
Let’s consider the point C(8/5, y) divides the line AB in ratio of P : 1

Now, by section formula, coordinates of point P (X, Y) which lies between two points (x₁, y₁), (x₂, y₂) will be given by:

P (X,Y) =

here, point divides the line in ratio of m_{1 :} m₂

Let’s transfer values in the above formula, we get:

For x coordinate:

∴ 8 (P + 1) = 5 (2 P + 1)

∴ 8 P + 8 = 10 P + 5

∴ 8 – 5 = 10 P – 8 P

∴ 3 = 2 P

∴ P =

∴ P : 1 = 3 : 2

Therefore, the point C divides the line AB in ratio of 3:2.

Similarly, for y coordinate:

y =

=

By substituting value of P = , we get:

y =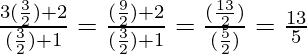

Therefore, value of y is .

Please press the heart button, if you liked the solution.