Q) For what value of x, is the median of the following frequency distribution 34.5 ?

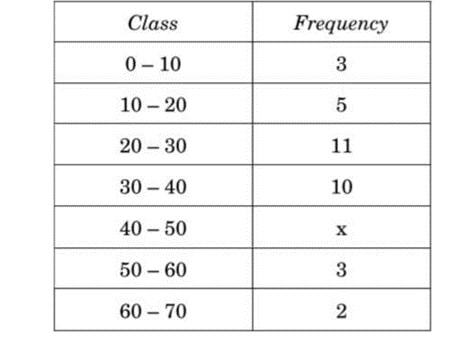
Ans: Let’s re-organize the data in the frequency table to find out each part:

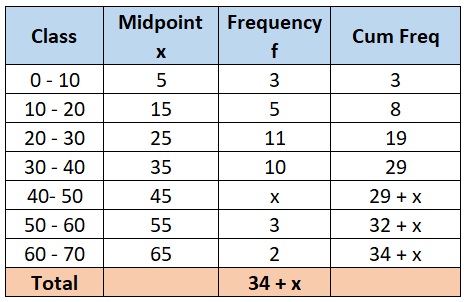
To find the median, we need to identify middle value of the data. Let’s rearrange the data:

• First, we need to find the cumulative frequency in the frequency table to find the median. Its shown in last column.
• Next, Total number of frequencies = 34 + X. It shown in the last row of middle column.
• Next, we need to identify Median Class. Since the Median class is the class where the cumulative frequency crosses 50% of the half the total number of frequencies, here in the table, Cumulative frequency of 34 + X is crossing 50% of frequency i.e. 17 + , at class “30-40”.
• Hence, our Median class = 30-40
• Next, To find the median, we use the formula:

Median = L+ \times h

Here:

L = Lower boundary of the median class = 30

n = Total number of sub-divisions = 34 + X

= Cumulative frequency of the class before the median class = 19

f = Frequency of the median class = 10

h = Class width = 40 – 30 = 10

hence, the Median = 30 + x 10

⇒ 34.5 = 30 + – 19

⇒ 23.5 =

⇒ 47 = 34 + X

⇒ X = 13

Therefore, for median 34.5, value of X is 13.