Q) From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

Ans:

Let’s start from the diagram for the question:

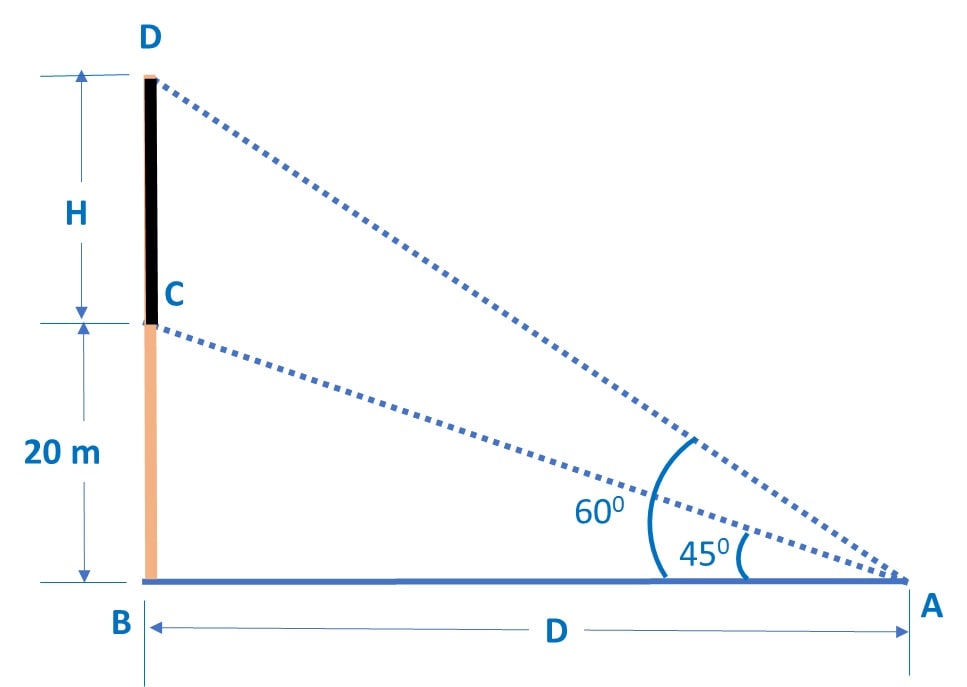
Let ‘s take BC be the building of 20 m CD as the tower of height H m

Point A is D distance away from B.

Step 1: Let’s start from In Δ ABC, tan ∠ CAB =

∴ tan 45⁰ =

∴ 1  =

∴ D = 20 …………. (i)

Step 2: Next, in Δ ABD, tan ∠ DAB =

∴ tan 60⁰ =

∴ √3 =

∴ D √3 = H + 20  …………. (ii)

Step 3: From equation (i) and equation (ii), we get:

D √3 = H + 20

∴ 20 √3 = H + 20    (∵ D = 20)

∴ 20 √3 – 20 = H

∴ H = 20(√3 – 1)

∴ H =20 (1.732 – 1)

∴ H = 14.64 m

Therefore, height of the tower is 14.64 m

Please do press “Heart” button if you liked the solution.