Q) If sin θ = ![]() , prove that
, prove that ![]() .
.
Ans: Let’s start LHS:
![]()
= 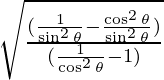
= 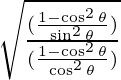
∵ 1- cos2 θ= sin2 θ
∴ LHS = 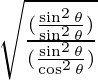
= 
= ![]()
= ![]() = cot θ
= cot θ
∵ sin θ = ![]() ∴ cot θ =
∴ cot θ = ![]()
∴ LHS = ![]()
= RHS
Hence Proved !
Q) If sin θ = ![]() , prove that
, prove that ![]() .
.
Ans: Let’s start LHS:
![]()
= 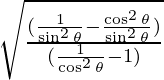
= 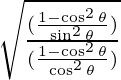
∵ 1- cos2 θ= sin2 θ
∴ LHS = 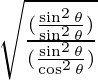
= 
= ![]()
= ![]() = cot θ
= cot θ
∵ sin θ = ![]() ∴ cot θ =
∴ cot θ = ![]()
∴ LHS = ![]()
= RHS
Hence Proved !