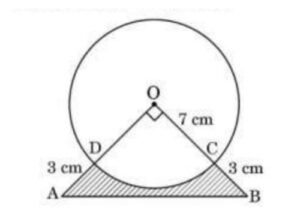
Q) In an annual day function of a school, the organizers wanted to give a cash prize along with a memento to their best students. Each memento is made as shown in the figure and its base ABCD is shown from the front side. The rate of silver plating is Rs. 20 per cm².

Based on the above, answer the following questions:

(i)   What is the area of the quadrant ODCO?

(ii)   Find the area of Δ AOB.

(iii) (a) What is the total cost of silver plating the shaded part ABCD?

OR

(iii) (b) What is the length of arc CD?

Ans: 

VIDEO SOLUTION

STEP BY STEP SOLUTION

(i) Area of the quadrant ODCO:

We know that, Area of a sector of a circle = 

Area of the quadrant ODCO = x 7 x7 x

= 22 x 7 x

= 38.5 cm²

(ii) Area of Δ AOB:

Line OA = OD + AD = 7 + 3 = 10 cm

Line OB = OC + CB = 7 + 3 = 10 cm

Since ∠ OAB = 90⁰

Area of Δ AOB = x OA x OB = x 10 x 10

• Area of Δ AOB = 50 cm²

(iii) (a) Total cost of silver plating the shaded part ABCD:

Area of shaded area ABCD = Area of Triangle ABC – Area of sector ODCO

Therefore, Area of shaded area ABCD = 50 – 38.5 = 11.5 cm²

Since, Cost of silver plating is Rs. 20/cm²

Hence, cost of silver plating area ABCD = 11.5 x 20 = Rs. 230

Therefore, Hence, cost of silver plating area ABCD = Rs. 230/-

(iii) (b) Length of Arc CD:

Length of arc is given by = 2

Length of arc CD = 2 x x 7 x

= 2 x 22 x

= 11 cm

Therefore, Length of arc CD is 11 cm