In the given figure, a circle centered at origin O has radius 7 cm.

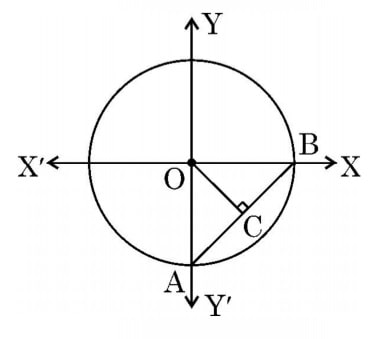
Q) In the given figure, a circle centered at origin O has radius 7 cm, OC is median of Δ OAB. Find the length of median OC.

Ans:

Step 1: In the given circle, OA and OB are the radii of the same circle and they intersect at 90 degrees (coordinates)

Δ AOB, by Pythagoras theorem, AB = $\sqrt{OA^2 + OB^2}$

= $\sqrt {(7)^2 + (7)^2}$ = 7√2

Step 2: Since OC is median of Δ AOB and perpendicular on AB, hence by triangle property, it will bisect AB

∴ AC = BC = $\frac{7 \sqrt 2}{2}$

Step 3: In Δ OAC, OC² = OA² – AC²

∴ OC² = 7² – $(\frac{7 \sqrt 2}{2})^2 = 49 - \frac{49}{2} = \frac{49}{2}$

∴ OC = $\sqrt {\frac{49}{2}}$

∴ OC = $\frac{7}{\sqrt 2}$

Please do press “Heart” button if you liked the solution.

Contact us