Q) In the given figure, ABC is a triangle in which ∠B = 900, BC = 48 cm and AB = 14 cm. A circle is inscribed in the triangle, whose centre is O. Find radius r of in-circle.
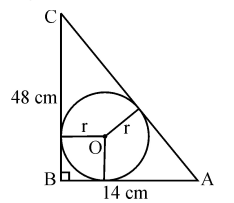
Ans:
By Pythagorus theorem,
AC = ![]()
= ![]()
= ![]()
= 50 cm
Method 1:
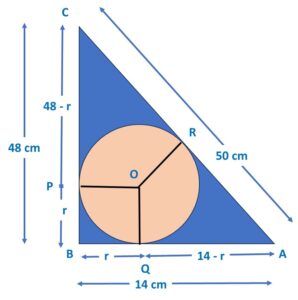
OP = OQ (radius of a circle)
BP = BQ (tangents from external point)
Since OPBQ is a square, therefore, BP = OQ = r
and BQ = OP = r
Now ∵ BQ = r ∴ AQ = 14 – r
∵ AQ = AR (tangents from external point)
∴ AR = 14 – r …. (i)
Similarly, ∵ BP = r, ∴ CP = 48 – r
∵ CP = CR (tangents from external point)
∴ CR = 48 – r …… (ii)
Since, AC = AR + CR
∴ 50 = (14 – r) + (48 – r)
∴ 50 = 62 – 2 r
∴ 2 r = 12
∴ r = 6 cm
Method 2: The radius of in-circle of a right angled triangle is given by:
r = ![]()
= ![]()
= ![]()
= 6 cm
