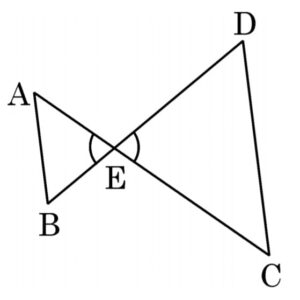
Q)  In the given figure, EA/EC = EB/ ED , prove that ΔEAB ~ ΔECD

Ans:

Step 1: It is given that:

∴  by cross multiplying, we can say that:

Step 2: Let’s look at Δ EAB and Δ ECD:

∠ AEB = ∠ DEC    (∵ Vertically Opposite Angles)

Step 3: Let’s compare Δ EAB and Δ ECD:

Now we have:

and ∠ AEB = ∠ DEC

∴ by SAS similarity criterion, we get:

Δ EAB ~ Δ ECD

Hence Proved!

Please do press “Heart” button if you liked the solution.