Q) In the given figure PA, QB and RC are each perpendicular to AC. If AP = x, BQ = y and CR = z, then prove that 1/x + 1/z = 1/y

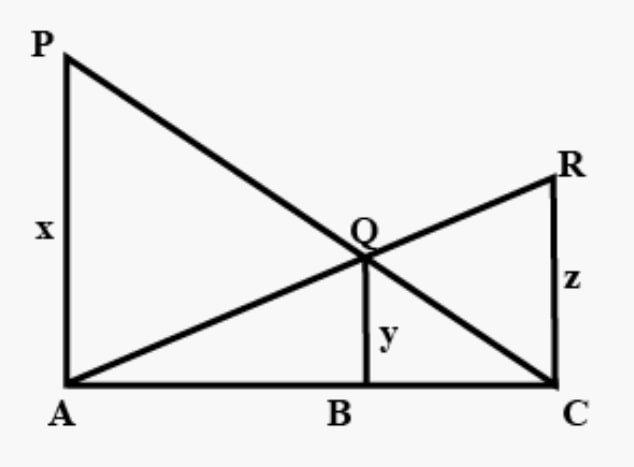
Ans:

Step 1: In Δ APC and Δ BQC,

∠ PCA = ∠  QCB  (common angle)

∠ PAC = ∠  QBC  (90⁰)

By AA identity, Δ APC ~ Δ BQC

Hence,    

   ………….. (i)

Step 2: In Δ RCA and Δ QBA,

∠ RAC = ∠  QAB  (common angle)

∠ RCA = ∠  QBA  (90⁰)

By AA identity, Δ RCA ~ Δ QBA

Hence,    

   ………….. (ii)

By adding equations (i) and (ii), we get:

Dividing by x y z on both sides, we get:

Hence Proved !

Please do press “Heart” button if you liked the solution.