Q) In what ratio does the X-axis divide the line segment joining the points(2, – 3) and (5, 6)? Also, find the coordinates of the point of intersection.

Ans: Let’s draw the diagram to solve:

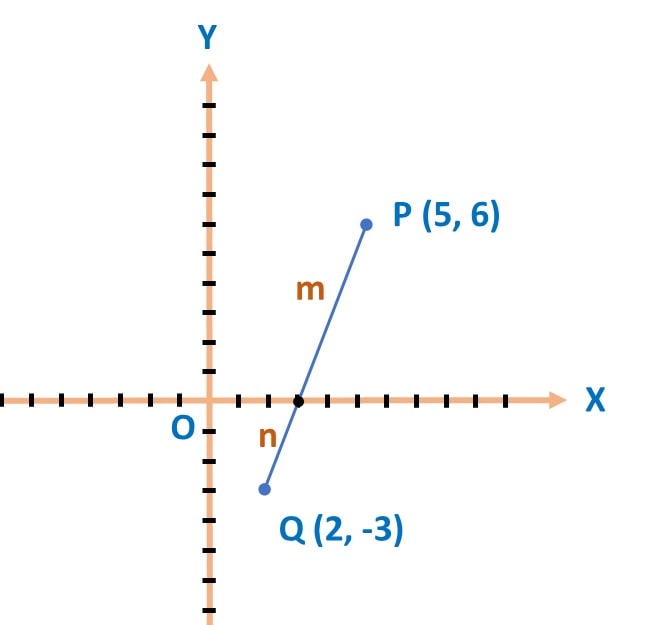
(i) Ratio of division:

We know that the value of y-coordinate on X- axis is always 0

It is given that X-axis intersects the line connecting points P &Q, hence the value of y-coordinate of intersection point A will be 0.

∴ we can consider the coordinates of point A as (x, 0)

Next, let’s consider that the line PQ is divided in the ratio of m : n.

We know that, by section formula, if a point (x, y) divides the line joining the points (x₁, y₁​) and (x₂​, y₂​) in the ratio m : n, then the coordinates of intersection point (x, y) is given by:

,

Here, it is given that

P (2, – 3) = (x₁, y₁​)

Q (5, 6) = (x₂​, y₂​),

Let’s consider line is divided in the ratio of m : n

Hence the y-coordinate of point A:

y =

∴  0 =

∴ – 3 m + 6 n = 0 

∴ 3 m = 6 n

∴ m = 2 n

∴ m : n = 2 : 1

Therefore, the line is divided in the ratio of 2 : 1.

(ii) Coordinates of intersection point:

From the section formula, let’s find the value of x coordinate:

x =

∴ x =

∴ x = = 3

Since, value of y coordinate is 0 (being on X-axis)

Therefore the coordinates of intersection point A are (3, 0).

Please press the “Heart”, if you like the solution.