Q) In what ratio is the line segment joining the points (3, – 5) and (- 1, 6) divided by the line y = x ?

Ans: 

Method 1:

Step 1:  Now, by section formula, coordinates of point P (X, Y) which lies between two points (x₁, y₁), (x₂, y₂) will be given by:

P (X,Y) =

here, point divides the line in ratio of m_{1 :} m₂

Step 2: Now if the given points A (3, -5) and B(- 1, 6) are divided in the ratio of m : n, then:

coordinates of dividing point (x, y) = 

=

Step 3: Next, since this point lies on line y = x, this point will satisfy the equation

∴

∴ 6 m – 5 n = 3 n – m

∴ 7 m = 8 n

∴ m : n = 8 : 7

Therefore, the line segment divides the line in ratio of 8:7.

Method 2: Let’s plot the points on the graph:

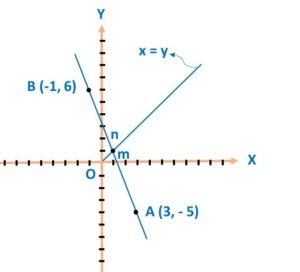
Let’s make an equation of the line passing through points A and B:
y – Y₁ = (x – X₁)
y – (- 5) = (x – 3)
y + 5 = (x – 3)
– 4 (y + 5) = 11 (x – 3)
– 4 y – 20 = 11 x – 33
– 2 y + 6 = x – 5
11 x + 4 y = 13

Since this line intersects the line x = y, hence for the intersection point, abscissa and ordinate values will be equal i. e. x = y
Hence, 11 x + 4 (x) = 13 or 15 x = 13 or x = ; Similarly, 11 (y) + 4 y = 13 or 15 y = 13 pr y = .
Let’s say this is point C.

Next, we calculate distance of C from A and B respectively. Hence AC = = = = =

Next, BC = = = = =

Let’s check the ratio of these lengths. Hence AC:BC = = = = = 8:7.

Therefore the ratio m:n = 8 :7

How to check your answer:

Here, Let’s consider that the ratio of m:n = 8:7. Hence, the coordinates of intersection point are: = = = .

Since this point lies on the line y = x, hence its abscissa and ordinate values should be equal. We can see that this is true for our coordinates of the intersection point, hence our answer is correct.

Please press the “Heart”, if you liked the solution.