Q) In 𝛥ABC, P and Q are points on AB and AC respectively such that PQ is parallel to BC.
Prove that the median AD drawn from A on BC bisects PQ.

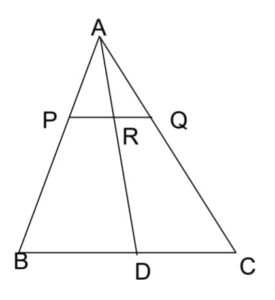
Ans:

Step 1: Let’s start from comparing triangles △ APR and △ ABD. Here we have:

∠ APR  = ∠ ABD      (corresponding angles, ∵ PQ ǁ BC)

∠ PAR = ∠ BAD      (Common angle)

∴ by AA similarity criterion, we get:

∴ △ APR ~ △ ABD

∴ …. (i)

Similarly, we compare △ ARQ and △ ADC:

∠ AQR  = ∠ ACD      (corresponding angles, ∵ PQ ǁ BC)

∠ QAR = ∠ CAD      (Common angle)

∴ by AA similarity criterion, we get:

∴ △ AQR ~ △ ACD

∴ …. (ii)

Step 3: Next, by comparing equations (i) and (ii), we get:

  …. (iii)

It is given that AD is the median in Δ ABC

∴ BD = CD

Hence, equation (iii) becomes:

or PR = QR

Therefore, median AD is also bisecting PQ….  Hence Proved !

Please do press “Heart” button if you liked the solution.