Q) India meteorological department observes seasonal and annual rainfall every year in different sub-divisions of our country.

It helps them to compare and analyse the results. The table given below shows sub-division wise seasonal (monsoon) rainfall (mm) in 2018:

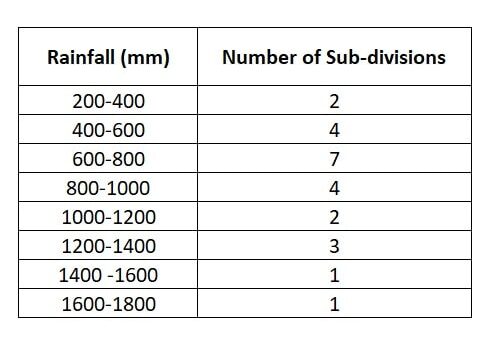
Based on the above information, answer the

following questions:

(I) Write the modal class.

(II) Find the median of the given data.

OR

(II) Find the mean rainfall in this season.

(III) If sub-division having at least 1000 mm rainfall during monsoon season, is considered good rainfall sub-division, then how many sub-divisions had good rainfall?

Ans:

VIDEO SOLUTION

STEP BY STEP SOLUTION

Let’s re-organize the data in the frequency table to find out each part:

i) Since the modal class is the class with the highest frequency.

In the given question, class “600-800” has the highest frequency. And 7 sub-divisions are experiencing this rainfall.

Hence, class “600-800” is the modal class.

ii) Median or Mean Rainfall:

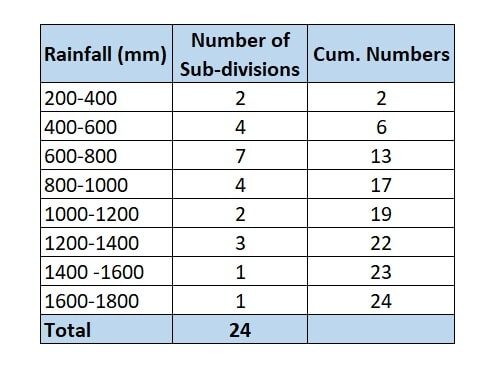
To find the median, we need to identify middle value of the data. Let’s rearrange the data:

• First, we need to find the cumulative frequency in the frequency table to find the median. Its shown in last column.
• Next, Total number of sub-divisions or Sum of the frequencies = 24. It shown in the last row of middle column.
• Next, we need to identify Median Class. Since the Median class is the class where the cumulative frequency crosses 50% of the half the total number of sub-divisions, here in the table, Cumulative frequency of 13 is crossing 50% of frequency i.e. 12, at class “600-800”. Hence, our Median class = 600-800 mm
• Next, To find the median, we use the formula:

Median = L+x h

Here:

L = Lower boundary of the median class = 600

n = Total number of sub-divisions = 24

= Cumulative frequency of the class before the median class = 2 + 4 = 6

f = Frequency of the median class = 7

h = Class width = 800 – 600 = 200

hence, the Median = 600 + x 200

⇒ 600 + [(12-6)] x

⇒ 600 +

⇒ 600 + 171.428

⇒ 771.43 mm

Therefore, Median = 771.43 mm

OR

(II) Find the mean rainfall in this season.

Let’s re-arrange the data with midpoint of each class, frequency, and multiply midpoint with frequency:

We know that, mean of grouped data is given by:

Mean of grouped data =

Therefore, Mean = = 850

Hence, the mean rainfall in the season is 850 mm 

(III) Sub-divisions with Good Rainfall:

Given that sub-divisions with at least 1000 mm rainfall are considered to have good rainfall. These sub-divisions are from 1000-1200 mm onwards.

Hence, To find the number of sub-divisions with good rainfall, we add up the frequencies of the classes from 1000-1200 mm to 1600-1800 mm.

Good rainfall sub-divisions = 2 + 3 + 1 + 1 = 7

Therefore, 7 sub-divisions had good rainfall during the monsoon season.