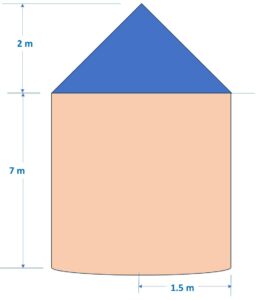
Q) Metallic silos are used by farmers for storing grains. Farmer Girdhar has decided to build a new metallic silo to store his harvested grains. It is in the shape of a cylinder mounted by a cone.

Dimensions of the conical part of a silo is as follows:  Radius of base = 1.5 m, Height = 2 m

Ans: Let’s draw a diagram to better understand the question:

(i) slant height of the conical part:

We know that the slant height of the conical part is given by:

L = , where R is radius of the base and H is the height

Now we are given, R = 1.5 m and H = 2 m,

Therefore, slant height, L =

=

=  = 2.5 m

Therefore the slant height of the conical part is 2.5 m

(ii) Curved surface area of conical part:

We know that the Curved surface area of the conical part is given by:

A = π R L, where R is radius of the base and L is the slant height

Now we are given, R = 1.5 m and we calculated L = 2.5 m

Therefore, Area A = π (1.5) (2.5) = 3.75 π

= 3.75 x

= 11.79 m²

Therefore the Curved surface area of the conical part is 11.79 m²

(iii)(A) Cost of metal sheet for cylindrical part:

To calculate the cost of the metal sheet used in curved cylindrical part, we need to calculate the area of cylindrical part.

We know that the Curved surface area of the cylindrical part is given by:

A = 2 π R H, where R is radius of the cylinder and H is the height of the cylinder

Now we are given, R = 1.5 m and height H = 7 m

Therefore, Area of cylinder = 2 π (1.5) (7) = 21 π

= 21 x

= 66 m²

Now the cost of 1 m² metal is Rs. 2,000

Hence, cost of 66 m² = 66 x 2,000 = 1,32,000

Therefore cost of the metal used to make Curved surface area of the cylindrical part is Rs. 1,32,000

(iii) (B) Find the total capacity of one silo to store grains.

The capacity of the silo = volume of cylindrical part + volume of conical part

= π R² H + π R² h

= π R² (H + h)

Here we have following values: Radius of cylinder & Cone, R = 1.5 m, Height of cylinder, H = 7 m and Height of cone, h = 2 m

The capacity of the silo = π R² (H + h)

=

=

=

= 54.21 m³

Therefore total capacity of one silo is 54.21 m³

Please press the “Heart”, if you liked the solution.