Leave a Comment / trigonometry / By

Q) Prove that : \frac{\sin \theta - \cos \theta + 1}{\sin \theta + \cos \theta - 1} = \frac{1}{\sec \theta - tan \theta}

Ans: Let’s start with LHS:

LHS = \frac{\sin \theta - \cos \theta + 1}{\sin \theta + \cos \theta - 1}

= \frac{\sin \theta - \cos \theta + 1}{\sin \theta + \cos \theta - 1} \times \frac {\sin \theta + \cos \theta - 1}{\sin \theta + \cos \theta - 1}

= \frac{\sin \theta (\sin \theta + \cos \theta - 1) - \cos \theta (\sin \theta + \cos \theta - 1) + 1 (\sin \theta + \cos \theta - 1)}{\sin \theta (\sin \theta + \cos \theta - 1) + \cos \theta (\sin \theta + \cos \theta - 1) - 1 (\sin \theta + \cos \theta - 1)}

= \frac{(\sin ^2 \theta + \sin \theta \cos \theta - \sin \theta - \sin \theta \cos \theta - \cos ^2 \theta + \cos \theta + \sin \theta + \cos \theta - 1)}{(\sin ^2 \theta + \sin \theta \cos \theta - \sin \theta + \sin \theta \cos \theta + \cos ^2 \theta - \cos \theta - \sin \theta - \cos \theta + 1)}

= \frac{(\sin ^2 \theta + \cancel {\sin \theta \cos \theta} - \cancel {\sin \theta} - \cancel {\sin \theta \cos \theta} - \cos ^2 \theta + \cos \theta + \cancel {\sin \theta} + \cos \theta - 1)}{(\sin ^2 \theta + \sin \theta \cos \theta - \sin \theta + \sin \theta \cos \theta + \cos ^2 \theta - \cos \theta - \sin \theta - \cos \theta + 1)}

= \frac{(\sin ^2 \theta - \cos ^2 \theta + 2 \cos \theta - 1)}{(\sin ^2 \theta + \cos ^2 \theta + 2 \sin \theta \cos \theta - 2 \sin \theta - 2 \cos \theta + 1)}

∵ sin2 θ + cos2 θ = 1

∴ LHS = \frac{(\sin ^2 \theta - \cos ^2 \theta + 2 \cos \theta - (\sin ^2 \theta + \cos ^2 \theta))}{(1 + 2 \sin \theta \cos \theta - 2 \sin \theta - 2 \cos \theta + 1)}

= \frac{(\sin ^2 \theta - \cos ^2 \theta + 2 \cos \theta - \sin ^2 \theta - \cos ^2 \theta)}{(2 + 2 \sin \theta \cos \theta - 2 \sin \theta - 2 \cos \theta)}

= \frac{(\cancel {\sin ^2 \theta} - 2 \cos ^2 \theta + 2 \cos \theta - \cancel {\sin ^2 \theta})}{(2 - 2 \sin \theta - 2 \cos \theta + 2 \sin \theta \cos \theta)}

= \frac{( 2 \cos \theta - 2 \cos ^2 \theta)}{(2(1 - \sin \theta) - 2 \cos \theta (1 - \sin \theta))}

= \frac{2 \cos \theta (1 - \cos \theta)}{2(1 - \sin \theta) ( 1 - \cos \theta)}

= \frac{ \cancel{2} \cos \theta \cancel{(1 - \cos \theta)}}{\cancel{2}(1 - \sin \theta) \cancel{( 1 - \cos \theta)}}

= \frac{(\cos \theta)}{(1 - \sin \theta)}

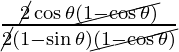
By dividing the numerator & denominator by cos θ, we get:

= \frac{\frac{\cos \theta}{\cos \theta}}{\frac{1 - \sin \theta}{\cos \theta}}

= \frac{\frac{\cos \theta}{\cos \theta}}{\frac{1}{\cos \theta} - \frac{\sin \theta}{\cos \theta}}

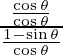
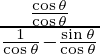
= \frac{1}{\sec \theta - \tan \theta} =  RHS

Hence Proved !

Please press “Heart” button if you like the solution. 

Related Posts

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top