Prove that : tan θ /(1 – cot θ) + cot θ / (1 tan θ) = 1 + sec θ cosec θ

Leave a Comment / trigonometry / By Sapling Academy

Q) Prove that : tan θ /(1 – cot θ) + cot θ / (1 – tan θ) = 1 + sec θ + cosec θ

Ans: Here, let’s start by simplifying the LHS in given equation:

LHS = $\frac{\tan \theta}{(1 - \cot \theta)} + \frac{\cot \theta}{(1 - \tan \theta)}$

= $\frac{(\frac{\sin \theta}{\cos \theta})} {1 - (\frac{\cos \theta}{\sin \theta})} + \frac{(\frac{\cos \theta}{\sin \theta})} {1 - (\frac{\sin \theta}{\cos \theta})}$

= $\frac{(\frac{\sin \theta}{\cos \theta})} {\frac{\sin \theta - \cos \theta}{\sin \theta})} + \frac{(\frac{\cos \theta}{\sin \theta})} {\frac{\cos \theta - \sin \theta}{\cos \theta})}$

= $\frac{\sin ^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} + \frac{\cos ^2 \theta}{\sin \theta (\cos \theta - \sin \theta)}$

= $\frac{\sin ^2 \theta}{\cos \theta (\sin \theta - \cos \theta)} - \frac{\cos ^2 \theta}{\sin \theta (\sin \theta - \cos \theta)}$

= $\frac{\sin ^3 \theta - \cos ^3 \theta}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$

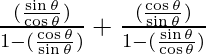
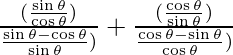
Now, we know that a^{3 –} b³ = (a – b) (a² + b² + a b)

Hence, sin³ θ – cos³ θ = (sin θ – cos θ ) (sin² θ + cos²θ + sin θ cos θ)

∵ sin² θ + cos²θ = 1

∴ sin³ θ – cos³ θ = (sin θ – cos θ ) (1 + sin θ cos θ)

By substituting this value in nominator of LHS, we get:

LHS = $\frac{\sin ^3 \theta - \cos ^3 \theta}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$

= $\frac{(\sin \theta - \cos \theta) (1 + \sin \theta \cos \theta)}{\sin \theta \cos \theta (\sin \theta - \cos \theta)}$

= $\frac{(1 + \sin \theta \cos \theta)}{\sin \theta \cos \theta}$

= $\frac {\sin \theta \cos \theta}{\sin \theta \cos \theta} + \frac{1}{\sin \theta \cos \theta}$

= 1 + sec θ cosec θ = RHS

Hence Proved !

Please do press “Heart” button if you liked the solution.

Leave a Comment Cancel Reply