Prove that : tan θ /(1 – cot θ) + cot θ / (1 tan θ) = 1 + tan θ + cot θ

Q) Prove that : tan θ /(1 – cot θ) + cot θ / (1 – tan θ) = 1 + tan θ + cot θ

Ans: Here, let’s start by simplifying the LHS in given equation:

LHS = $\frac{\tan \theta}{1 - \cot \theta} + \frac{\cot \theta}{1 - \tan \theta}$

= $\frac{\tan \theta}{1 - \frac{1}{\tan\theta}} + \frac{\frac{1}{\tan \theta}}{1 - \tan \theta}$

= $\frac{\tan ^2 \theta}{\tan\theta - 1} + \frac{\frac{1}{\tan \theta}}{1 - \tan \theta}$

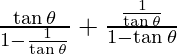
Let’s make the denominators equal:

LHS = $\frac{\tan ^2 \theta}{\tan\theta - 1} - \frac{\frac{1}{\tan \theta}}{\tan \theta - 1}$

= $\frac{\tan ^2 \theta - \frac{1}{\tan \theta}}{\tan \theta - 1}$

= $\frac{\tan ^3 \theta - 1}{\tan \theta (\tan \theta - 1)}$

We know that a^{3 –} b³ = (a – b) (a² + b² + a b)

Hence, tan³ θ – 1 = tan³ θ – 1³ = (tan θ – 1) (tan² θ + 1 + tan θ )

By substituting this value in nominator of LHS, we get:

LHS = $\frac {(\tan \theta - 1)(\tan ^2 \theta + 1 + \tan \theta)}{\tan \theta (\tan \theta - 1)}$

= $\frac {(\tan ^2 \theta + 1 + \tan \theta)}{\tan \theta}$

= $\frac{\tan ^2 \theta}{\tan \theta} + \frac{1}{\tan \theta} + \frac {\tan \theta} {\tan \theta}$

= tan θ + cot θ + 1

= 1 + tan θ + cot θ = RHS

Hence Proved !

Please do press “Heart” button if you liked the solution.

Contact us