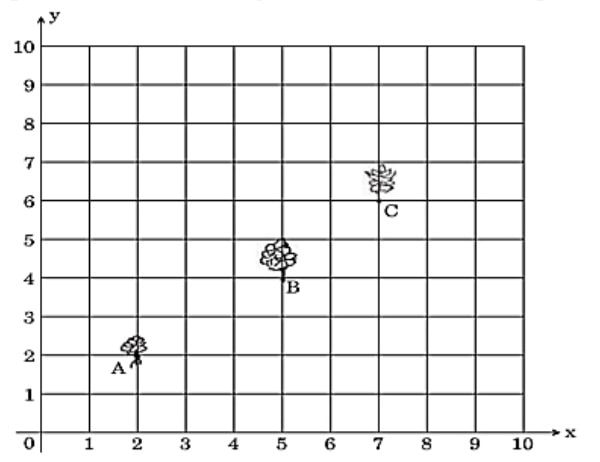
Q) Reena has a 10 m × 10 m kitchen garden attached to her kitchen. She divides it into a 10 × 10 grid and wants to grow some vegetables and herbs used in the kitchen. She puts some soil and manure in that and sow a green chilly plant at A, a coriander plant at B and a tomato plant at C. Her friend Kavita visited the garden and praised the plants grown there. She pointed out that they seem to be in a straight line. See the below diagram carefully:
i. Find the distance between A and B.
ii. Find the mid-point of the distance AB.
iii. Find the distance between B and C.
iv. Find the mid point of BC.
Ans:
1. Distance between A and B:
Step 1: From the diagram, Coordinates of point A: (2, 2)
Coordinates of point B: (5, 4)
Step 2: We know that the distance between two points P (X1, Y1) and Q (X2, Y2) is given by:
PQ = ![]()
∴ Distance AB = ![]()
∴ AB = ![]()
∴ AB = ![]()
Therefore, the distance between points A and B is √13 m.
2. Mid point of AB:
Step 3: Now we have coordinates of point A (2, 2) and Point B (5, 4)
∵ We know that the coordinates of midpoint of 2 coordinates (X1, Y1) and (X2, Y2) given by:
(X, Y) = ![]()
∴ Coordinates of midpoint of A (2, 2) and B (5, 4) = ![]()
= ![]()
Therefore, the coordinates of midpoint of AB are (![]() , 3).
, 3).
3. Distance between B and C:
Step 4: From the diagram, Coordinates of point B: (5, 4)
Coordinates of point C: (7, 6)
Step 5: By putting values in distance formula (explained in step 2), we get:
∴ Distance BC = ![]()
∴ AB = ![]()
∴ AB = ![]()
Therefore, the distance between points A and B is 2 √2 m.
4. Mid point of BC:
Step 3: Now we have coordinates of point B (5, 4) and Point C (7, 6)
By putting values in distance formula (explained in step 3), we get:
Coordinates of midpoint of B (5, 4) and C (7, 6) = ![]()
= ![]() = (6, 5)
= (6, 5)
Therefore, the coordinates of midpoint of AB are (6, 5).
Please press the “Heart”, if you liked the solution.
