Q) Rinku was very happy to receive a fancy jumbo pencil from his best friend Rohan on his birthday. Pencil is a basic writing tool, when sharpened its shape is a combination of cylinder & cone as given in the picture. 

Cylindrical pencil with conical head is a common shape worldwide since ages. Commonly pencils are made up of wood & plastic but we should promote pencils made up of eco-friendly material (many options available in the market these days) to save environment. 

The dimensions of Rinku’s pencil are given as follows: Length of cylindrical portion is 21cm. Diameter of the base is 1 cm and height of the conical portion is 1.2 cm. Based on the above information, answer the following questions:

1. Find the slant height of the sharpened part.
2. Find curved surface area of sharpened part (in terms of 𝜋).
3. Find the total surface area of the pencil (in terms of 𝜋).
4. The pencil’s total height decreases by 8.2 cm after sharpening it many times, what is the volume of the cylindrical part of the shortened pencil (in terms of 𝜋)?

Ans: Let’s draw a diagram to better understand the question:

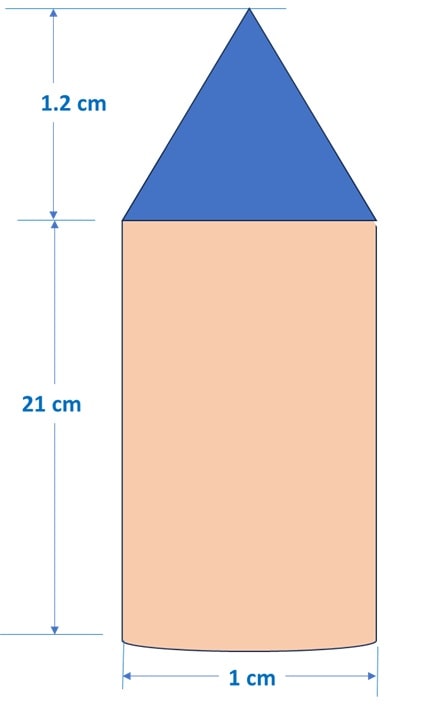
(i) slant height of the sharpened part:

We know that the slant height of the conical part is given by:

L = , where R is radius of the conical base and H is the cone’s height

Now we are given, R = 0.5 cm and H = 1.2 cm,

Therefore, slant height, L =

=

= = 1.3 cm

Therefore the slant height of the sharpened conical part is 1.3 cm

(ii) Curved surface area of sharpened part:

We know that the Curved surface area of the conical part is given by:

A = π R L, where R is radius of the conical base and L is the slant height

Now we are given, R = 0.5 cm and we calculated L = 1.3 cm

Therefore, Area A = π (0.5) (1.3) = 0.65 π cm²

Therefore, the Curved surface area of the sharpened part is 0.65 π cm²

(iii) Total surface area of pencil:

Total surface area of the pencil = CSA of conical top + CSA of cylinder + Area of circular base

= π R_cone L + 2 π  R_cylinder H_cylinder + π  R ²

= 0.65 π + 2 π  (0.5) (21) + π (0.5) ²

= 0.65 π + 21 π +  0.25 π

= 21.90 π cm ²

Therefore, the Curved surface area of the cylindrical part is 21.90 π cm²

(iv) Volume of the shortened pencil:

After sharpening height of the pencil is reduced by: 8.2 cm

New height of the pencil = 21 – 8.2 = 12.8 cm

Volume of the new cylindrical part of the shortened pencil = π R² H

Radius of cylinder, R = 0.5 cm, New height of cylinder, H = 12.8 cm

The volume of new pencil = π (0.5)² (12.8) = 3.2 π m³

Therefore, Volume of the new cylindrical part of the shortened pencil is 3.2 π m³ 

Please press the “Heart”, if you liked the solution.