Q) Sides AB, BC and the median AD of ∆ ABC are respectively proportional to sides PQ, QR and the median PM of another
∆ PQR. Prove that ∆ ABC ~ ∆ PQR
Ans:
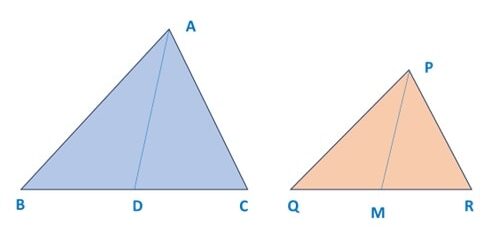
Given that, In Δ ABC and Δ PQR,
![]()
Since AD is median of BC, hence BC = 2BD
Similarly, PM is median of QR, hence QR = 2QM
![]()
or ![]()
![]() Δ ABD ~ Δ PQM
Δ ABD ~ Δ PQM
Hence, ∠ B = ∠ Q ……………. (i)
Now In Δ ABC and Δ PQR, we know that,
or ![]() (given)
(given)
∠ B = ∠ Q from equation (i)
Now by SAS similarity rule,
Δ ABC ~ Δ PQR……….. Hence proved !
Please press the “like” button if you like the solution.
