Q) The angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the distance of the cloud from the point of observation is ![]() .
.
Ans:
Step 1: Let’s draw a diagram for the given question:
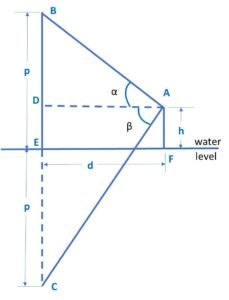
Here, point of observation is A, cloud is at point B and cloud’s reflection is at point C.
Here, let’s consider the height of AF is h and line AD or Line EF is d, height of cloud from water level is p and CE is also p (reflection).
We need to find length of line AB.
Step 2: Let ‘s start with Δ ADB,
tan ∠ DAB = ![]()
∴ tan α = ![]()
∴ p – h = d tan α
∴ p = h + d tan α ……….. (i)
Step 3: Next in Δ ADC,
tan ∠ DAC = ![]()
∴ tan β = ![]()
∴ p + h = d tan β
∴ p = d tan β – h ….. (ii)
Step 4: From equations (i) and (ii), we compare values of p:
h + d tan α = d tan β – h
∴ 2 h = d tan β – d tan α
∴ 2 h = d (tan β – tan α)
∴ d = ![]() ……… (iii)
……… (iii)
Step 5: Δ ADB, cos ∠ DAB = ![]()
∴ cos α = ![]()
∴ AB = d sec α …… (iv)
Step 6: By substituting value of d from equation (iii), in equation (iv), we get:
AB = d sec α
∴ AB = ![]()
∴ AB = ![]()
Hence Proved !
Please press “Heart” button if you like the solution.
