Q) The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 30 seconds, the angle of elevation changes to 30°. If the jet plane is flying at a constant height of 3600 √3 m, find the speed of the jet plane.
Ans: Let’s start with the diagram for this question:
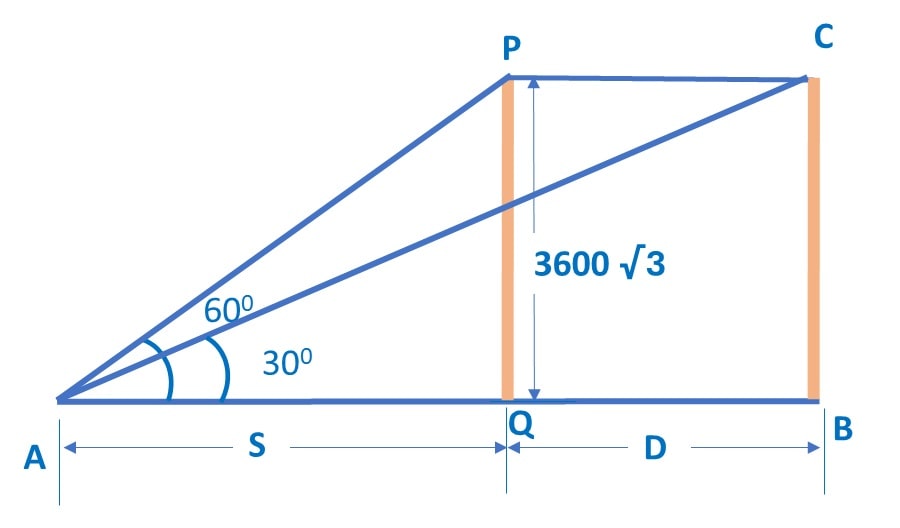
Step 1: Let’s start from Δ APQ, tan A = tan 60° = 
∴ √3 = 
∴ S = 3600 m
Step 2: Next, we take Δ ABC, tan A = 
∴ tan 30 = 
∴ 
∴ S + D = 3600 √3 x √3 = 10800
∴ D = 10800 – S = 10800 – 3600 [∵ S = 3600 from part (i)]
∴ D = 7200 m
Step 3: Given that the jet plane covered the distance D in 30 seconds
and we calculated D = 7200 m
∴ Speed of the Jet Plane = 
= 
meter /second
= 
km / hour
= 864 km/hr
Therefore, speed of the jet plane is 864 km/hr
Please do press “Heart” button if you liked the solution.