The angle of elevation of the top of a tower 24 m high from the foot

/ trigonometry applications / By Sapling Academy

Q) The angle of elevation of the top of a tower 24 m high from the foot of another tower in the same plane is 60°. The angle of elevation of the top of second tower from the foot of the first tower is 30°. Find the distance between two towers and the height of the other tower. Also, find the length of the wire attached to the tops of both the towers.

Ans:

VIDEO SOLUTION

STEP BY STEP SOLUTION

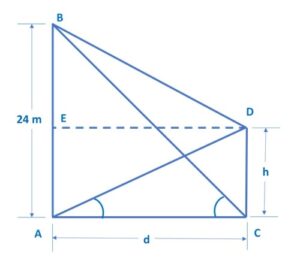
Let’s start with a diagram for the question:

Let AB and CD be the towers where AB is first tower of 24m height

Let Height of the other tower be h and distance between both of the towers be d

Step 1: Calculation for Distance between the towers:

In Δ BAC, tan 60° = $\frac{24}{d}$

∴ √3 = $\frac{24}{d}$

∴ d = $\frac{24}{\sqrt 3}$

∴ d = $\frac{8 \times 3}{\sqrt 3}$

∴ d = 8√3 m

Therefore, the distance between the two towers is 8√3 m

Step 2: Calculation for height of another tower:

In Δ DAC, tan 30° = $\frac{h}{d}$

∴ h = $\frac{d}{\sqrt3}$

∴ h = $\frac{8\sqrt 3}{\sqrt3}$

∴ h = 8 m

Therefore, the height of other tower is 8 m

Step 3: Calculation for Length of the wire between tops of two towers:

In Δ BDE, BD² = BE² + DE²

∴ BD² = (BA – CD)² + AC² (∵ BE = BA – DC and DE = AC)

∴ BD² = (24 – 8)² + (8 √3)²

∴ BD² = 16² + (8 √3)²

∴ BD² = 256 + 192 = 448

∴ BD = √448 = 8√7 m

Therefore, the length of wire between tops of two towers is 8√7 m

Please press the “Heart” button if you like the solution.