Q) The angle of elevation of the top of a vertical tower from a point P on the ground is 60°. From another point Q, 10 m vertically above the first point P, its angle of elevation is 30°. Find:
(a) The height of the tower.
(b) The distance of the point P from the foot of the tower.
(c) The distance of the point P from the top of the tower.

Ans:

Let’s start from the diagram for the question:

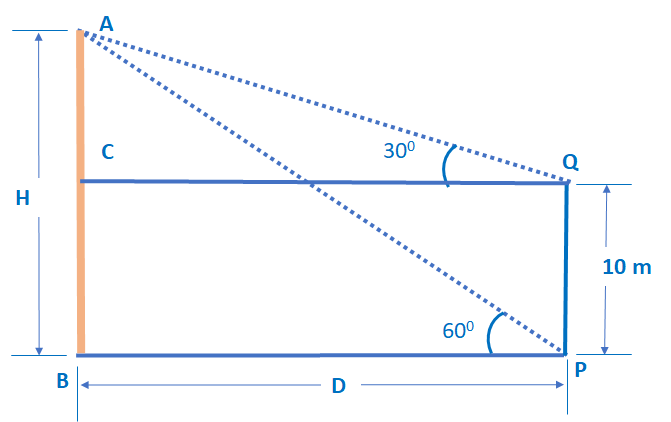
Let ‘s take AB as a tower with the height as ‘H’ and the distance of point P from the foot of the tower as ‘D’. Given that the Point Q is 10 m high vertically above the point P. Angles from both points are also plotted.

(a) The height of the tower (H):

In Δ ABP, tan P =

Since, ∠ APB = 60⁰ , AB = H, BP = D

∴ tan 60⁰ = √3 =

∴ D = …………. (i)

(Note: Here we calculate D in terms of H, because when we substitute value of D, we will get all H terms together and value of H will be calculated.)

Next, in Δ ACQ, tan Q =

Since, ∠ AQC = 30⁰ , AC = H – 10, CQ = BP = D

∴ tan 30⁰ =

∴ D = (H – 10) √3 …………. (ii)

By substituting, value of D from equation (i) in equation (ii), we get:

  = (H – 10) √3

H = 3 (H – 10)

H = 3H – 30

2H = 30 or H = 15

Therefore, the height of the tower AB is 15 m.

(b) The distance of the point P from the foot of the tower (PB):

from equation (i),

D =

We just calculated, H = 15 m, therefore,

D = = 5 √3

Therefore, the distance of the point P from the foot of the tower (PB) is 5 √3 m.

(c) The distance of the point P from the top of the tower (AP).

In Δ ABP, sin P =

Since, ∠ APB = 60⁰ , AB = H = 15,

∴ sin 60⁰ = 

AP √3 = 30

AP = = 10√3

Therefore, the distance of the point P from the top of the tower is 10 √3 m.