Leave a Comment / polynomials, quadratic / By

Q) The speed of a motor boat is 20 km/hr. For covering the distance of 15 km the boat took 1 hour more for upstream than downstream.

The speed of a motor boat is 20 km/hr.

1. Let speed of the stream be x km/hr. Then speed of the motorboat in upstream will be
a) 20 km/hr           b) (20 + x) km/hr         c) (20 – x) km/hr            d) 2 km/hr

2. What is the relation between speed, distance and time?
a) speed = (distance )/time         b) distance = (speed )/time
c) time = speed x distance         d) speed = distance x time

3. Which is the correct quadratic equation for the speed of the current?
a) x2 + 30x − 200 = 0                     b) x2 + 20x − 400 = 0
c) x2 + 30x − 400 = 0                     d) x2 − 20x − 400 = 0

4. What is the speed of current?
a) 20 km/hour       b) 10 km/hour           c) 15 km/hour             d) 25 km/hour

5. How much time boat took in downstream?
a) 90 minute          b) 15 minute               c) 30 minute                 d) 45 minute

Ans:

1. 
∵ Upstream speed = Boat’s speed – Stream’s speed
∴ Upstream speed = 20 km/hr – x km/hr
= (20 – x) km/hr
Therefore, option (c) is correct.
2. 
Speed is always given by \frac{Distance}{Time}
Therefore, option (a) is correct.
3.
Step 1: By given information, Boat’s speed = 20 km/hr and Stream’s speed = X km/hr
∴ Upstream speed = (20 – X) km/hr
and Downstream speed = (20 + X) km/hr
Step 2: Since distance travelled is D
Since, time taken to travel = \frac{Distance}{Speed}
∴ Time taken upstream = \frac{15}{20 - \times}
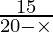
Similarly,  Time taken downstream = \frac{15}{20 + \times}
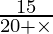
Step 3: By given condition: Upstream time is 1 hour more than downstream time
∴ \frac{15}{20 - \times} = 1 + \frac{15}{20 + \times}
∴ \frac{15}{20 - \times} = \frac{20 + \times + 15}{20 + \times}
∴ \frac{15}{20 - \times} = \frac{35 + \times}{20 + \times}
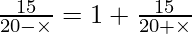
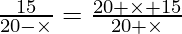
∴ 15 (20 + X) = (35 + X)(20 – X)
∴ 300 + 15 X =  700 + 20 X – 35 X – X2
∴ X2 + 30 X – 400 = 0
Therefore, option (c) is correct.
4. Let’s solve above quadratic equation:
By mid term splitting we get:
∴ X2 + 40 X – 10 X – 400 = 0
∴ X (X + 40) – 10 (X + 40) = 0
∴ (X + 40) (X – 10) = 0
∴ X = 10 and X = – 40
Here, we reject X = – 40 because the speed value has to be positive and accept X = 10
Hence, speed of the current is 10 km/hr

Therefore, Option (b) is correct

5.  As calculated in part 3, Time taken downstream = \frac{15}{20 + \times}
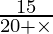
Since X = 10, ∴ the Time taken downstream
= \frac{15}{20 + 10} = \frac{15}{30}
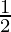
= \frac{1}{2} = 0.5 hrs = 30 mins
Therefore, option (c) is correct.
Check: Time taken upstream = \frac{15}{20 - \times} = \frac{15}{20 - 10} = \frac{15}{10} = 1.5 hrs
We just calculated: Time taken downstream = 0.5 hrs
Here, upstream time = downstream time + 1
Since it matches with the given condition in question, hence our answer is correct. 

Please press the “Heart” button if you like the solution.

Related Posts

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top